How To Find Atoms Per Cm2 Of A Plane

Atomic Packing Factor (APF) tells you what percent of an object is made of atoms vs empty infinite. Y'all tin can think of this equally a volume density, or as an indication of how tightly-packed the atoms are.

For quick reference, I accept created a tabular array below of atomic packing cistron (APF) values for common crystal structures. Subsequently in the article, I explain step-past-step how to calculate them.

Crystal Construction	Atomic Packing Gene
Simple Cubic (SC)	52%
Body-Centered Cubic (BCC)	68%
Face up-Centered Cubic (FCC)	74%
Hexagonal Close-Packed (HCP)	74%

Atomic packing cistron (APF) of common crystal structures.

Calculating the atomic packing factor for a crystal is elementary: for some repeating volume, calculate the volume of the atoms within and split by the total book.

$APF=\frac{volume\:taken\:by\:atoms}{total\:volume}$

Usually, this "repeating book" is just the book of the unit jail cell. The unit jail cell is defined as the simplest repeating unit in a crystal.

Bold all atoms have the aforementioned size, and are arranged in a repeating crystal lattice,

$APF=\frac{N_{atoms}V_{atom}}{V_{unit\:cell}}$

where $N$ means number and $V$ ways volume.

For a more complicated description of having multiple kinds of atoms, click here to aggrandize.

If you accept multiple kinds of atoms, you need to include the number and volume of each atom.

$APF=\frac{\sum _iN_iV_i\:\:}{\:V_{total}}$

where $V_i$ is the book of each blazon of cantlet. In metals there is commonly only one atom, but in a ceramic, suppose at that place are 3 kinds of atoms: $A$ , $B$ , and $C$ . The expanded version would look like this:

$APF=\frac{N_AV_A+N_BV_B+N_CV_C\:}{\:V_{unit\:cell}}$

Additionally, atomic packing cistron uses the hard sphere model. That means each atom has the volume of a sphere. Assuming the atoms are difficult spheres with radius $r$ in a cubic unit cell with lattice parameter $a$ ,

$APF=\frac{\frac{4}{3}\pi \:r^3\cdot N_{atoms}}{a^3}$

This might exist a niggling hard to anticipate, then let'south start past dropping into ane- and 2-dimensions.

ane-Dimensional Packing Cistron: Linear Density

Since we're in 1D, formulas with book don't apply. Don't worry! If yous sympathize the concept, you won't need a formula at all.

Recall, we want to find the infinite taken by atoms compared to the total space. Since we're in ane-dimension, "space" ways "length." We tin can say that 1-dimensional packing is a linear density or line density.

For any detail management, you need to draw a line and determine what percentage of the line is covered past a circle.

Of course, you tin't just draw any random line. The line needs to exist along the crystal "cell."

If y'all're not sure how to do this in 1-dimension, click here to aggrandize.

This picture may make information technology seem like the unit cell is just an atom, but that'southward only true in the shut-packed direction. Usually, it makes the most sense to draw the unit cell so that a half-atom sticks out on both ends (like the red unit cell).

See, if the atoms are non "shut-packed," the unit prison cell will need to have more than infinite. In other words, the lattice volition be larger than the footing.

(In the arrangement above, the lattice and basis are the same size, which is why you define the unit jail cell effectually the circle with no actress space).

As long as the line you draw is a valid representation of the overall crystal symmetry, any line volition piece of work!

Simply take the length of the line covered by circles, and divide by the total length of the line.

The maximum packing cistron is 1, which means 100% of the line is occupied by a circle.

If yous had a packing gene larger than one, it would hateful that somehow multiple circles overlapped on the aforementioned department of the line.

two-Dimensional Packing Factor: Planar Density

In 2 dimensions, space is surface area, rather than a line or a book. Determining the packing factor works exactly the same way, however. Nosotros telephone call this the planar density or surface area density.

Simply find a crystallographically repeating area (the unit jail cell volition e'er work) and carve up that expanse by the surface area covered by the circles.

Look at that! These two arrangements accept the same packing. Any thought why that is . . . ?

Now, permit'south motion into 3 dimensions and take a await at how to calculate APF for the 4 common unit cells.

Unproblematic Cubic (SC) Lattice Length and APF

As earlier, we desire to know how much of the crystal space is occupied by atoms vs empty space. We have entered 3-dimensions (the real globe), so space is volume. To perform this adding, we need to know the book of a cube and the volume of a sphere.

Book of a cube: $V_{cube}=a^3$ , where $a$ is the length of a side.

Volume of a sphere: $V_{sphere}=\frac{4}{3}\pi r^3$ , where $r$ is the radius of the sphere.

Now, we have ii variables: $r$ (radius of cantlet) and $a$ (side length of cube).

It turns out that $r$ and $a$ can be written in terms of each other.

A simple cubic (SC) unit of measurement cell is a cube with an atom on each corner of the cube. The size of the cube will be determined by the size of the atoms!

As you can see, for the simple cubic cell, the lattice parameter is just twice the radius. Now, in terms of the radius, nosotros can say that the book of the cube is:

Each cantlet is a sphere, so the volume per atom is:

$V_{sphere}=\frac{4}{3}\pi r^3$

where $r$ is the radius of the sphere.

But, how many atoms do nosotros have per unit prison cell? At first glance, information technology looks like there are viii atoms: on on each corner of the jail cell.

However, yous demand to consider that when you stack unit cells to make the full crystal, each corner is shared with eight cells. And then each of the 8 atoms contributes ⅛ of its total volume. In total, there is i total atom per unit jail cell.

Now if nosotros split the volume of an atom by the volume of the unit of measurement prison cell, the diminutive packing factor for a simple cubic crystal is:

$APF_{SC}=\frac{\frac{8}{8}\cdot \frac{4}{3}\pi r^3}{^{\left(2r\right)^3}}=\frac{\pi }{6}\approx 52\%$

Body-Centered Cubic (BCC) Lattice Length and APF

To calculate the atomic packing factor, what practice we need first? The volume of the atoms, and the volume of the unit cell.

For some radius of the atoms, we tin can calculate their volume using

$V_{sphere}=\frac{4}{3}\pi r^3$

The volume of the cube is $a^3$ in terms of the lattice constant $a$ , so let's write $a$ in terms of $r$ .

In a BCC crystal, the body diagonal is the shut-packed direction. I promise this is clear in the image below.

Since the body diagonal is the close-packed direction, the atoms touch each other. That ways the body diagonal will be a multiple of the diminutive radius. In this case, the body diagonal is $4r$ .

Now, it'due south time to employ the pythagorean theorem (you could also use 3D vector math, only if you don't know what that is, the trigonometry is not so complicated).

First, brand a triangle with the body diagonal as the hypotenuse. This is the green line in the image in a higher place. One of your triangle legs volition be the cube'due south side, $a$ . The other leg volition be the confront diagonal. Yous can use any variable you like for this length; I will choose $d$ .

Using the pythagorean theorem, $a^2+d^2=(4r)^2$ .

Now, let's discover $d$ . We tin can make another triangle from a different 3D view; this time our triangle has $d$ on the hypotenuse and $a$ for both legs.

Again using the pythagorean theorem, we see $a^2+a^2=d^2$ , or $d^2=2a^2$ .

Now we can plug $d^2$ into our kickoff pythagorean theorem.

Then,

$a=\frac{4}{\sqrt{3}}r$

At present that we tin write the volume of the cube in terms of the diminutive radius, the rest is like shooting fish in a barrel!

Nosotros but demand to figure out how many atoms are in each unit prison cell. As in the simple cubic example, in that location are 8 corner atoms. Each corner atom contributes ⅛ of its volume to the unit jail cell, so that'south equal to 1 whole atom.

Additionally, there is an cantlet in the middle of the jail cell. Since that entire atom is inside the cell, it fully contributes its volume.

In total, there are 2 atoms in the BCC unit cell. If nosotros divide the volume of 2 atoms by the volume of the unit jail cell ( $=a^3$ ), we discover that the atomic packing factor for a body-centered cubic crystal is:

$APF_{BCC}=\frac{\left(\frac{8}{8}+1\right)\frac{4}{3}\pi \:r^3}{\left(\frac{4}{\sqrt{3}}r\right)^3}=\frac{\sqrt{3}\pi }{\:8}\approx 68\%$

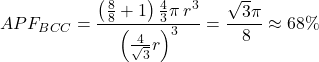
Confront-Centered Cubic (FCC) Lattice Length and APF

This should be familiar by now. Volume of the atoms divided by volume of the unit cell. Let's get the unit cell in terms of the diminutive radius!

In an FCC crystal, any face diagonal is the shut-packed direction. I hope y'all tin see this in the paradigm beneath.

The confront diagonal, therefore, has a length of $4r$ . Nosotros can get the lattice constant in terms of $r$ with a uncomplicated application of the pythagorean theorem.

Draw a triangle with the face diagonal (length = $4r$ ) as the hypotenuse. Both legs volition be $a$ .

So $a=2\sqrt{2}r$

$a^3$ will exist the volume of the unit prison cell, and so let's effigy out how many atoms are in the unit of measurement cell.

As nosotros've seen several times already, in that location will be 8 atoms on each corner, each contributing ⅛ of its total volume to the unit cell.

Additionally, there are 6 faces, with half an atom on each face (since faces are shared between ii cells, an atom on the face would contribute ½ of its volume to each cell).

In full, there are 4 atoms in the FCC unit prison cell. Dividing the volume of iv atoms by the volume of the cube gives united states of america the atomic packing gene for a face-centered cubic crystal:

$APF_{FCC}=\frac{\left(\frac{8}{8}+\frac{6}{2}\right)\frac{4}{3}\pi r^3}{\left(2\sqrt{2}r\right)^3}=\frac{\pi }{3\sqrt{2}}\approx 74\%$

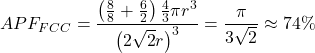
Hexagonal Close-Packed (HCP) Structure and APF

Now things get tricky.

The HCP crystal structure is not cubic. Luckily, it's still relatively like shooting fish in a barrel to visualize. It'south the natural way for humans to pack spheres.

Imagine you had to pack spheres into a box. You'd probably first past making a close-packed plane on the bottom of the box. And then, you'd start the next plane by placing a sphere at one off the depression points–in between iii spheres from the lesser aeroplane. Again, the 2d plane can exist arranged equally close-packed. The 3rd plane would expect exactly similar the 1st plane, the 4th plane would look exactly like the 2nd aeroplane, and so on.

This is the hexagonal close-packed lattice!

We call this unit of measurement cell "hexagonal close-packed" considering it looks like hexagonal planes. In almost all cases, we use the full HCP jail cell.

Notwithstanding, it's really possible to define a smaller unit of measurement prison cell from the same atomic arrangement. This is a rhombohedral cell. Since this is the smallest unit of measurement cell possible, we call this the HCP primitive unit cell.

Let'southward await at the archaic unit cell, considering it's simpler then it'south piece of cake to see the lattice parameters. Dissimilar a cube, there are really two independant lattice parameters.

Lattice parameter $a=b$ is the length between two touching atoms (so, twice the radius).

Lattice parameter $c$ is the height of the unit cell.

Past taking advantage of some trigonometry, it turns out that in an ideal HCP cell, there is a definite ratio of $c/a$ .

The Hexagonal Close-Packed c/a ratio

If you look at the central atom in the primitive cell, you tin can see that it has a distance $a$ between the atoms in the plane to a higher place and in the aeroplane below. If you projected the atom into ane of those planes, it would be exactly in the heart of three atoms.

This position is the middle of the equilateral triangle. If you're a big-time nerd and you lot already know how to summate the centroid of an equilateral triangle, keep reading.

Otherwise, click this push button.

Allow's describe a line between the heart of the triangle and one of its corners. We can call this $d$ . Because the angles of an equilateral triangle are all threescore°, the bending between $d$ and $\frac{a}{2}$ is 30°.

$\cos\left(30^{\circ} \right)=\frac{\left(\frac{a}{2}\right)}{d}$

$d=\frac{a}{\sqrt{3}}$

Now we can brand another triangle, between $d$ , $\frac{c}{2}$ , and $a$ .

$\left(d\right)^2+\left(\frac{c}{2}\right)^2=a^2$

$\left(\frac{a}{\sqrt{3}}\right)^2+\left(\frac{c}{2}\right)^2=a^2$

Which means that

$c=\sqrt{\frac{8}{3}}a$

$\frac{c}{a}\approx 1.633$

And remembering that $a=2r$ ,

$c=4\sqrt{\frac{2}{3}}$

Now that we take $a$ and $c$ , we can calculate the volume of the hexagonal unit cell.

Hexagonal Close-Packed Unit of measurement Prison cell Book

The hexagonal unit of measurement jail cell is just a hexagonal prism. You can google or memorize the answer quite hands, but in a examination you lot might go extra points for deriving the result yourself.

Click here to encounter 1 method.

Starting time by breaking this into parts. The volume of the hexagonal prism will exist the surface area of the hexagon * the height of the prism. The area of the hexagon is simply 6 equilateral triangles.

Let'south start past calculating the area of a single triangle. Any triangle'due south area is

$Area_{Triangle}=\frac{1}{2}Base\cdot Height$

Each side of the triangle has a length $a$ , so let's utilise that as our base. Now we demand to discover the height of the triangle.

One time over again, the pythagorean theorem saves the twenty-four hours! We tin can make correct triangle between $\frac{a}{2}$ , $a$ , and the height $h$ .

$\left(\frac{a}{2}\right)^2+h^2=a^2$

Which ways

$h=\sqrt{a^2-\left(\frac{a}{2}\right)^2}$

And so the area of the triangle is

$Area_{Triangle}=\frac{a}{2}\sqrt{a^2-\left(\frac{a}{2}\right)^2}=\sqrt{\frac{3}{4}}a^2$

And since there are 6 equilateral triangles per hexagon,

$Area_{Hexagon}=6Area_{Triangle}=\frac{3\sqrt{3}}{2}$

Multiplying this area by the height gives

$Volume_{HCP\:cell}=\frac{3\sqrt{3}}{2}a^2c$

and using $c=\sqrt{\frac{8}{3}}a$ and $a=2r$ ,

$Volume_{HCP\:cell}=24\sqrt{2}r^3$

Now that we know the volume of the HCP unit cell, we can calculate information technology's APF!

Hexagonal Shut-Packed Atomic Packing Fraction

The difficult function is backside united states. The atomic packing fraction (APF) is just the amount of atom within the unit jail cell, compared to the overall size of the unit cell.

For the HCP prison cell, at that place are 12 corner atoms. Each corner cantlet has ⅙ of its book inside the unit jail cell. To visualize this, imagine that you joined many unit cells together. Each corner atom would be shared between half-dozen other cells, so information technology contributes ⅙ to each.

There are 2 atoms on the face, which each contribute ½ of their volume.

There are 3 atoms in the center, which fully contribute their volume to the unit prison cell.

Altogether, that's 6 atoms per unit cell!

We know the volume of a sphere and we already calculated the volume of the unit prison cell, so

$APF_{HCP}=\frac{\left(\frac{12}{6}+\frac{2}{2}+\frac{3}{1}\right)\frac{4}{3}\pi \:r^3}{24\sqrt{2}r^3}=\frac{\pi \:}{3\sqrt{2}}\approx \:74\%$

Concluding Thoughts

That'due south it! Yous've learned how to calculate the lattice parameters and atomic packing fraction for simple cubic (SC), body-centered cubic (BCC), face-centered cubic (FCC), and hexagonal shut-packed (HCP) crystal systems.

Remember, APF is but the book of the atoms inside the unit of measurement cell, divided past the total book of the unit cell. Yous use this to summate the APF of any crystal system, even if it's non-cubic or has multiple kinds of atoms!

Source: https://msestudent.com/atomic-packing-factor/

Posted by: fernandezsucer1950.blogspot.com